Ekzercoj
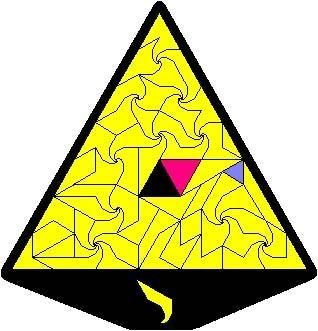
Inter la 54 pecoj de Polyspidrons, estas 2 egallateraj trianguloj (blua kaj ruĝa ĉisube) :
Se oni prenas la longon de latero de la eta triangulo kiel unito, latero de la granda estas longa je 
; por simpligi, ekde nun, mi notos r tiun nombron.
Se oni prenas la areon de la eta triangulo kiel unito, la areo de la granda estas r², tio estas 3 : tio estas logika, ĉar la granda triangulo estas 3-spidrono.
Ĉisube, oni vidas la 3 unuspidronojn je areo 1, la 10 duspidronojn je area 2, kaj la 41 trispidronojn je area 3 :
Se oni desegnas, sur la plato, kradon uzante la etan triangulon, oni obtenas :
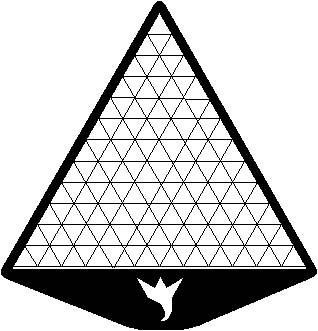
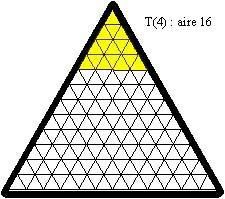
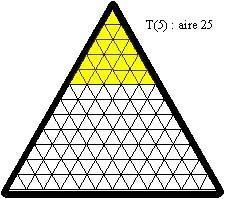
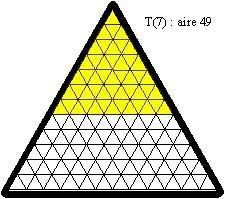
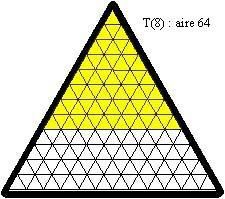
Tiu krado utilos al ni por ekzercoj ; ni flave kolorigu triangulojn por havi flavan triangulon je laterlongo 6 :
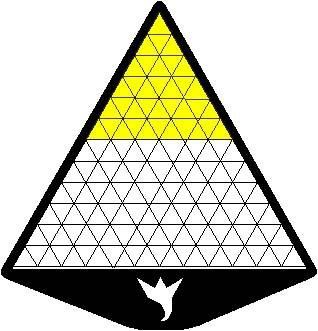
Tiu triangulo havas areon je 6² aŭ 36 ; oni povas kovri ĝin per plurspidronoj laŭ pluraj diversaj manieroj :
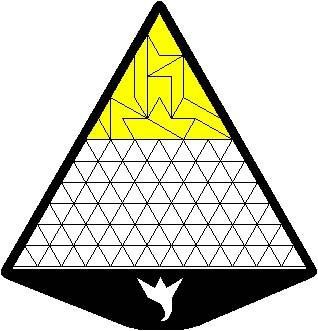
La ĉisupra solvo uzas nur plurspidronojn sen kapo ; estas solvoj per plurspidronoj havantaj unu aŭ pluraj kapoj : solvo kun 1 centra nodo da spidronoj, solvo kun 2 nodoj, solvo kun 3 nodoj kaj solvo kun 4 nodoj. La ĉisupran triangulon, kun latero je 6, mi notas T(6).
Vi povas provi T(1), T(2), ktp ... ĝis T(12), kiu estis Defio 001.
T(1) kompreneble estas tre simpla kaj la malfacileco iom post iom pligrandiĝas ...
Mi havas solvojn de T(1) ĝis T(12) ; mi metis solvon de T(12) je la 2007/11/22.
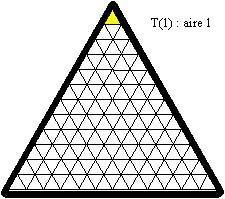aire = areo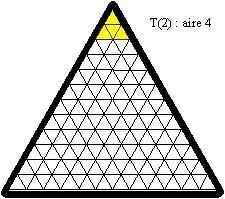 
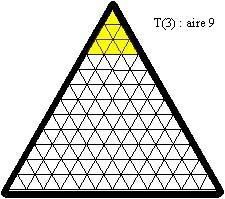
Defio 001
Se nun oni desegnas, sur la plato, kradon uzante la grandan triangulon, oni obtenas :
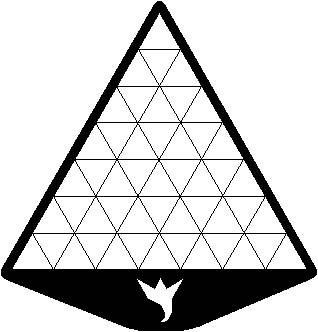
Laŭ la antaŭaj notacioj, oni povas provi kovri T(r), T(2r), T(3r), T(4r), T(5r) et T(6r) ; jen ekzemple solvo de T(2r) :
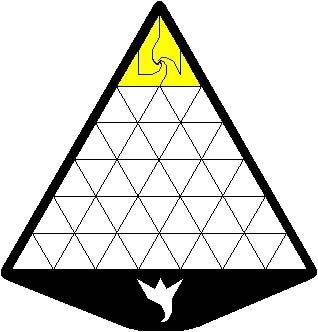
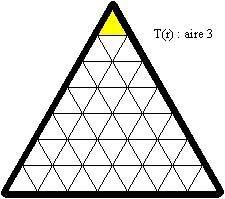
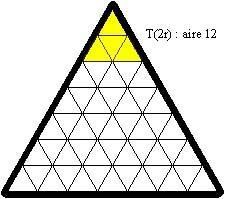
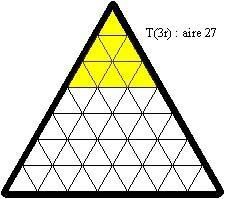
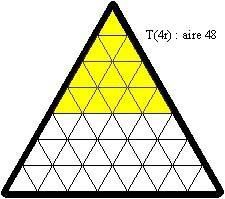
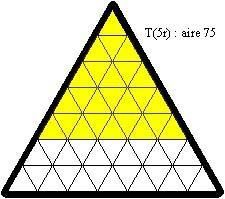
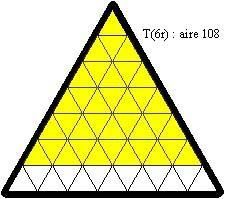
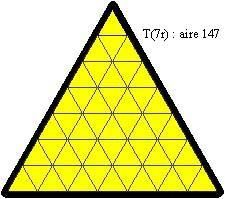
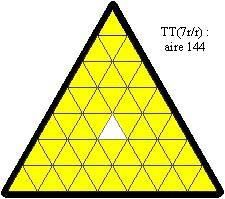
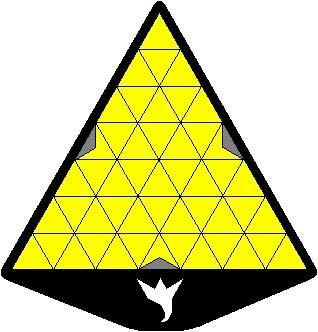
Sur la plato, tiu truo estas plenigita per 3 etaj nigraj trianguloj, similaj al unu el la unuspidronoj (ili estas grizaj ĉisube) :
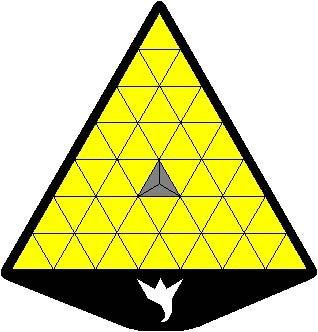
La pozicio de tiuj etaj trianguloj donos plurajn defiojn, kiuj aperos iom post iom sur la paĝoj de la defioj ; jen ekzemple la defio 028* :
