Spidrons de pentagone

L'hexagone et l'octogone avaient un nombre pair de sommets ; essayons avec un polygone régulier ayant un nombre impair de sommet ; prenons un pentagone :

 Relions ses sommets (en sautant un sommet à chaque fois) ; dans ce cas, tous les sommets sont atteints en une fois : 

Isolons le pentagone obtenu à l'intérieur :

Recommençons, avec ce pentagone, les 2 étapes décrites ci-dessus :

 

Puis, à nouveau, avec le nouveau pentagone :

Et ainsi de suite :

 

Colorions en jaune un spidron de pentagone :

Il y a, bien sûr, 5 spidrons de pentagone dans un pentagone :

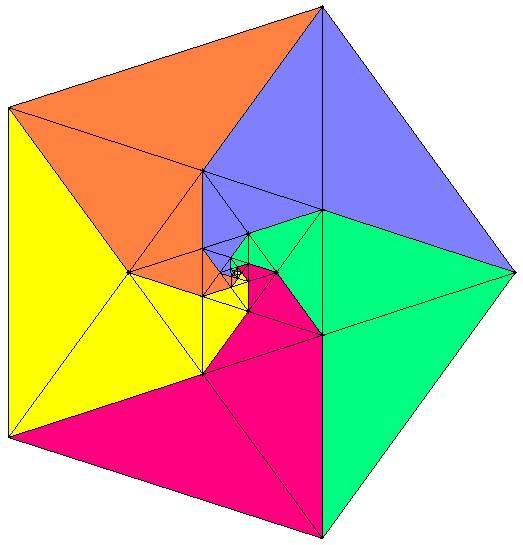
On m'a gentiment indiqué les travaux de Rinus Roelofs, Marc Pelletier et Walt van Ballegooijen sur les spidrons de pentagone :

voir http://www.rinusroelofs.nl/pr-spidron/spidron-03.html pour le premier

et http://www.szinhaz.hu/edan/spidronatlanta/ pour les deux autres (il faut aller dans Spidrose : je donnerai un lien plus précis lorsque je le récupérerai).

Je ne m'occupe pas du côté 3D car sur ces sites vous avez déjà des choses remarquables.