Spidrons d'hexagone
Voici une autre manière de construire un spidron* (ou plus exactement un demi-spidron) :
* Le Spidron est une création de Dániel Erdély.
(Pour un diaporama, cliquez ici):
Partons d'un hexagone :

Relions ses sommets (en sautant un sommet à chaque fois) :
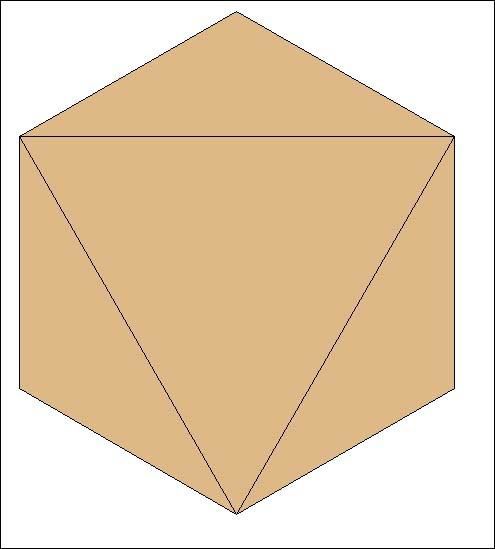
Relions ses autres sommets :

Isolons l'hexagone obtenu à l'intérieur :
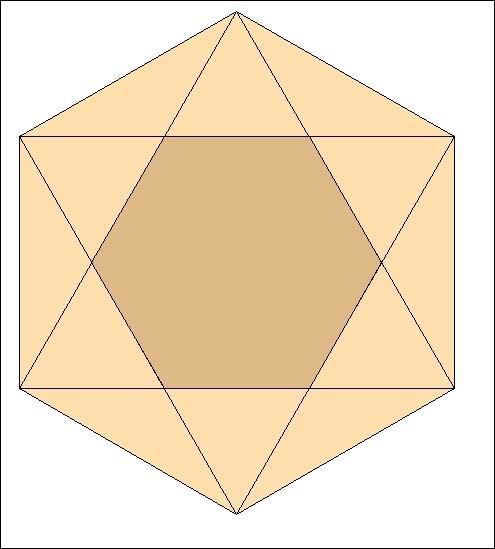
Recommençons, avec cet hexagone, les 3 étapes décrites ci-dessus :
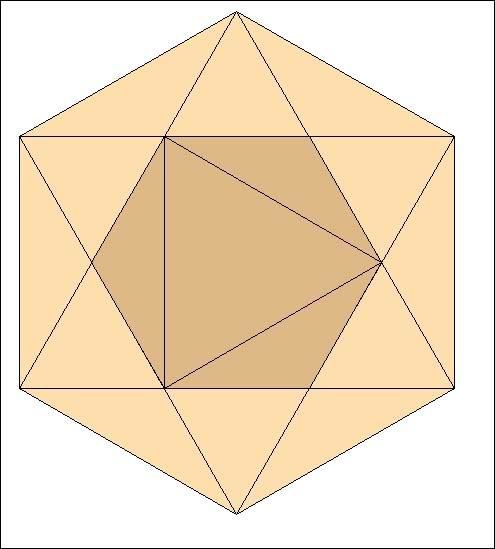
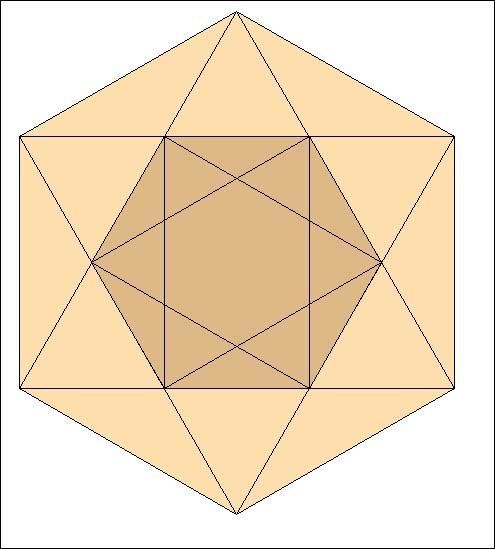
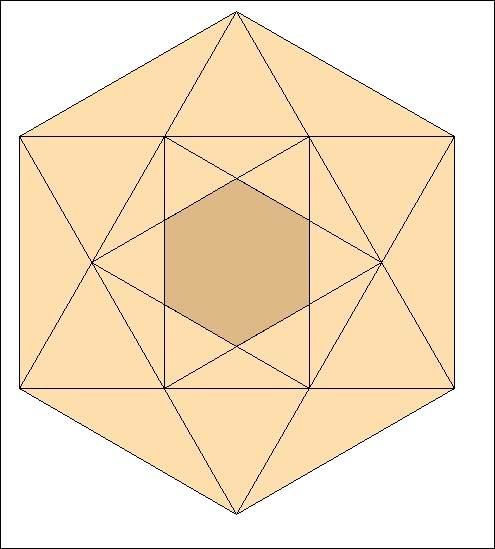
Puis à nouveau avec le nouvel hexagone :


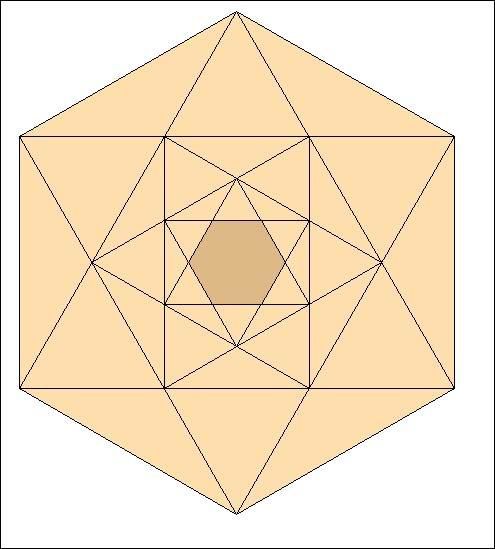
Et ainsi de suite :
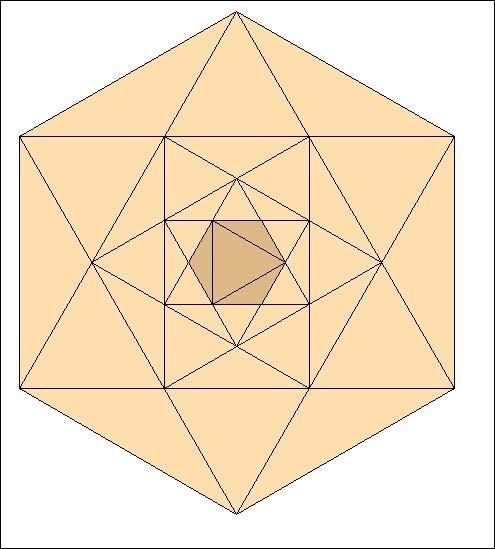
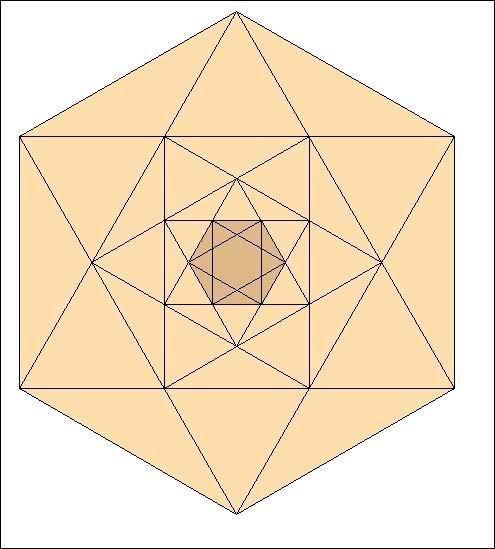

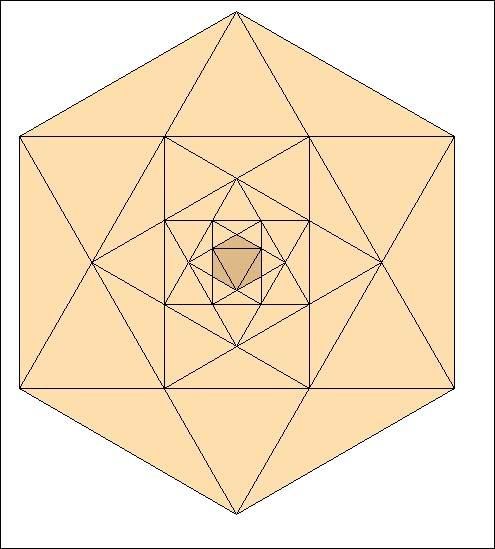

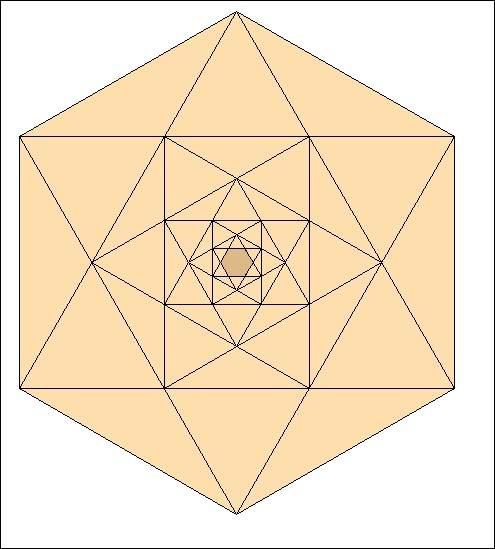
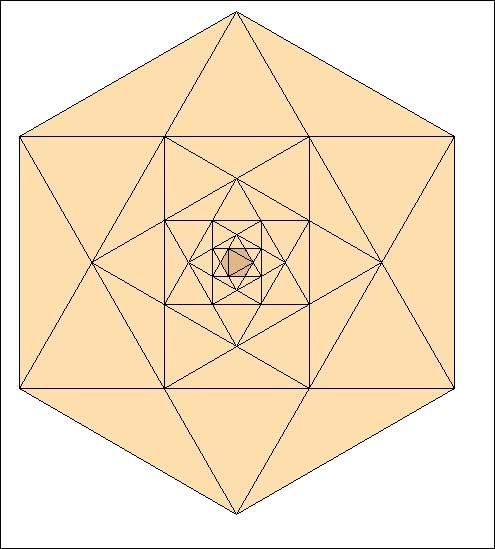
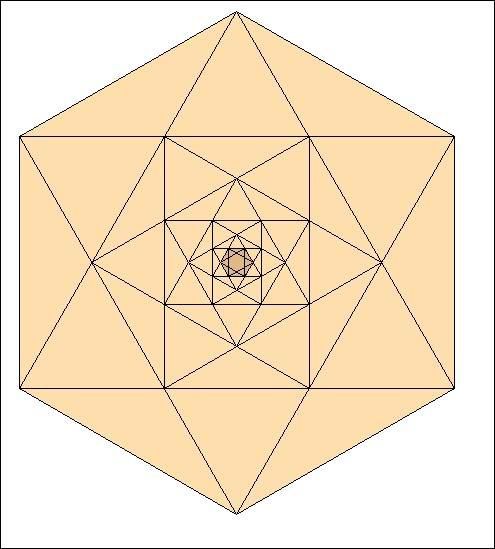

Sautons des étapes :

Colorions en jaune un demi-spidron :

Il y a 6 demi-spidrons dans l'hexagone :

Cette méthode de construction permet de comprendre comment les demi-spidrons s'agencent pour faire un hexagone ( Dániel Erdély appelle ses demi-spidrons des bras de spidron ; moi, je les appelle des têtes de spidron et j'appelle noeud de spidrons un hexagone formé de 6 têtes).
Dániel Erdély aurait pu décider d'appeler demi-spidrons les formes suivantes :

Mais il ne l'a pas fait et c'est tant mieux, car ses demi-spidrons ont des propriétés fabuleuses, surtout lorsqu'il les plie pour en faire des volumes époustouflants (voir Spidronatlanta et SpidroNew).
La méthode de construction ci-dessus ouvre des horizons si on essaie de la reproduire avec d'autres polygones que l'hexagone.
